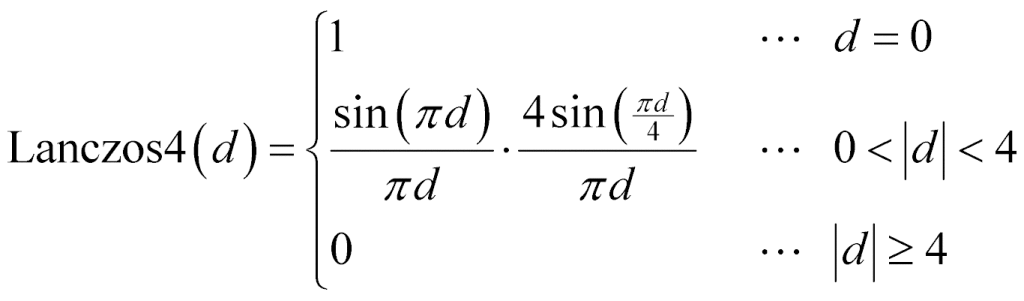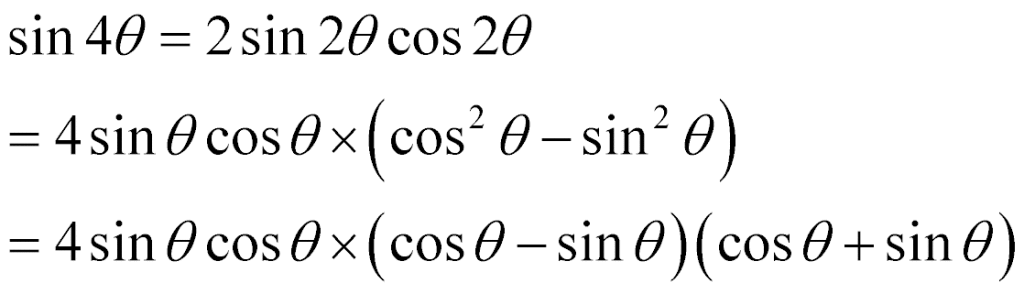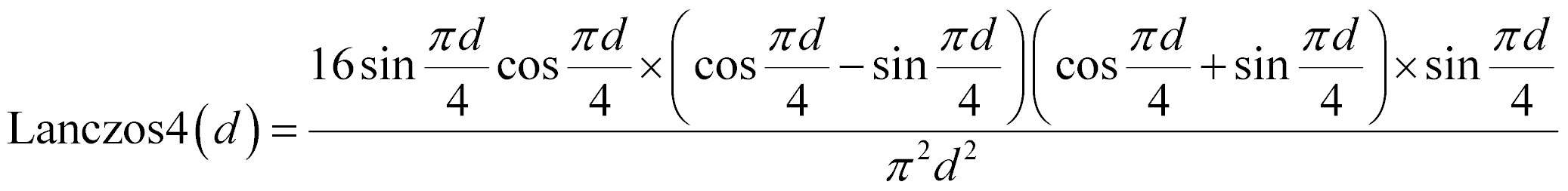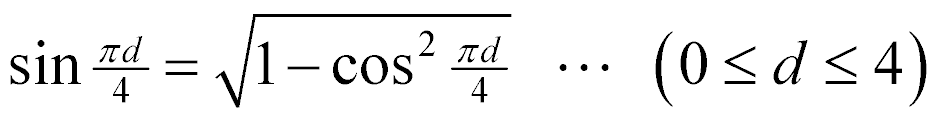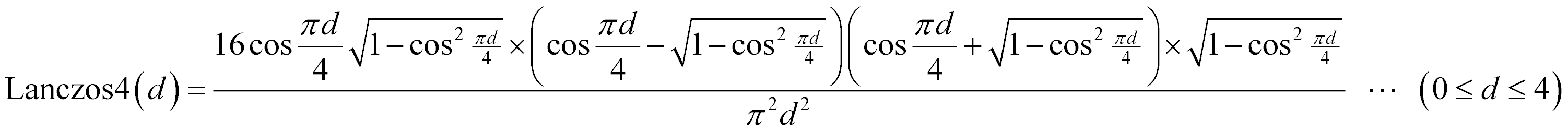【画像処理】Lanczos 4も高速化【式変形】

前回、Lanczos 3の式変形による高速化を紹介しました。スマホでの処理のように、高速なCPUであることが期待できない環境などで大きな効果が発揮されると思います。

さて、前回に引き続き、今回もLanczosの高速化を扱います。今回はLanczos 4です。Lanczos 3ができるなら、Lanczos 4だって出来るはずだとチャレンジしてみました。

まず、Lanczos 4の基本形の式がこちら。

なんとなく、倍角公式で何か出来そうなことが分かると思います。
そこで、4倍角の公式を作ります。

コレを利用して式変形すると

となるのですが、これでもまだ三角関数は2つ存在します。三角関数の2乗のルートで求められると考えるかもしれませんが、注意しなければならないのはコンピュータの求める平方根は常に正のみです。これが、三角関数を扱う際にネックとなるのです。それは、三角関数には負の値を返す可能性があるという点です。そのため、コンピュータで平方根を計算に用いる際には、こういう点にも配慮しなければなりません。

で、今回の式ですが、dには画素値同士の距離が入ります。計算方法にも依りますが、dが負の値になる可能性も存在します。dの値が負になると、この式の正弦関数は負の値を返すようになります。何の工夫もせず、そのまま余弦関数の2乗の平方根で値を求めた場合、正しい値を返さなくなります。

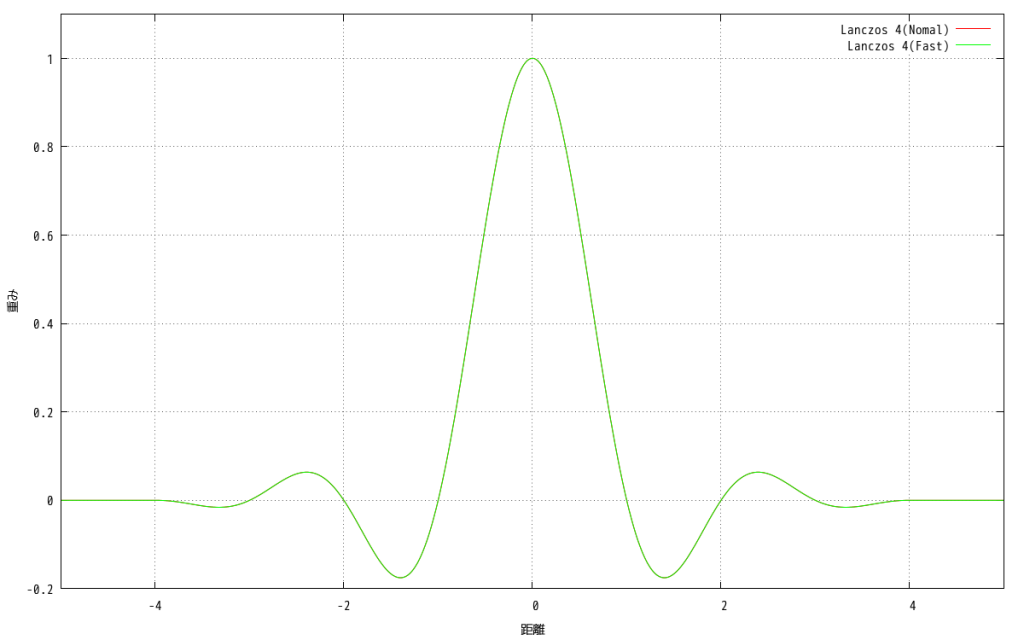
ここで、この式のグラフ上での形状に注目してみます。この式をグラフに出力するとこんな形になります。

Y軸について対称であることが分かります。つまり、Y軸から正の方向の値を取ろうと、負の方向の値を取ろうと、その絶対値が等しいならば全く同じ値を返すと言うことが分かります。

この式に与えられるdの値の範囲を正に制限すると、この正弦関数は正の値しか返さなくなります。つまり、余弦関数の2乗を利用して正しい値が求められると言うことです。

コレを使ってLanczos 4を更に変形させれば一つの三角関数だけでLanczos 4を求められるようになります。